Nonce-Sense

By: Hilbert
Cliffs: Server divulges $k$ which allows us to recover the private key. We can then sign any message ourselves and retrieve the flag.
The Challenge

Connecting to the instance we see this looks like a pretty straight forward crypto challenge setup.
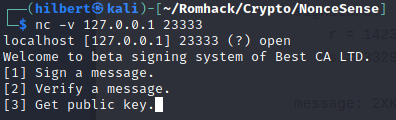
We can have the server sign or verify messages as well as provide us with some needed info. Typically that means we are going to have to figure out how to forge a signature for a specific message in order to get the flag, and if we look at the provided code, we see that is indeed the case. Here is the snippet from the code that handles verification
if dsa.verify(msg,r,s):
if msg == b'give me flag':
req.sendall(FLAG + b'\n')
exit(1)
Our goal is to verify ‘give me flag’ and we can have any message signed other than that one. Let’s look at the code and see what sticks out.
DSA in less than 6 lines (resolution dependant)
The Digital Signature Algorithm is a public-key cryptosystem. That means there are a pair of keys, a public key that is freely distributed and a private key that is kept secret. The purpose being that an entity can “sign” a message and anyone can use the resulting signature along with the public key and verify that signature was generated from that message using the associated private key. For such a scheme to be useful it’s important that the signature could only have originated using that specific message and private key and that it’s not feasible for anyone else to figure out the value of the private key or construct a different message that would validate with that signature.
Plan of attack
With the above in mind our focus when looking over the provided code should be on seeing if there is a way for us to figure out the generated private key, which would allow us to sign any message we want and have it be valid (like for example ‘give me flag’), or if we can somehow get the server to sign a different message, that will also give us a valid signature for ‘give me flag’.
Cryptography is hard, but still...
Cryptography is hard, it’s easy to make one small mistake the renders your implementation completely insecure. That’s why it’s important to use well vetted standardized cryptographic libraries, or to stick exactly to the documented protocols if you ever find yourself needing to implement it on your own. “Never roll your own crypto” is a widely known and used phrase. But at the very least, you should aim to understand the basics of whatever scheme you are working with, which does not appear to be the case by whoever at Best CA LTD wrote this function that generates an important variable!
def get_k(self, msg):
kmax = self.pKey.q
msg = [ a ^ b for (a,b) in zip(msg, cycle(KEY)) ]
msg = bytes(msg)
k = bytes_to_long(msg) % self.pKey.q
return msg, k
One of the factors that goes into keeping the private key secure is making sure that an attacker can never discover the value of $k$ which is a variable responsible for determining the value of $r$ in the signature $(r,s)$. If two different messages are ever signed by the same key using the same value for $k$ it is trivial to recover the private key. So $k$ needs to be random and selected from a large enough space that it can’t be brute forced and that it’s virtually impossible it will be repeated over the life of the key. Or $k$ can be generated in a deterministic manner such as from the hash of the message to be signed along with private key. This way $k$ is specific to each message so the signature for two differing messages will never originate from the same $k$ while still making it impossible to glean any information about what value for $k$ a given message will generate.
The latter seems to be what they were going for here
msg = [ a ^ b for (a,b) in zip(msg, cycle(KEY)) ]
The message is being XORed with some secret value KEY, and then
msg = bytes(msg)
k = bytes_to_long(msg) % self.pKey.q
return msg, k
the result is converted to an integer modulo $q$ but both the integer and the byte value are being returned, which if we look at the code that handles the user input for signing and follow the output of the above function
msg,k = dsa.get_k(msg)
h = bytes_to_long(h)
r, s = dsa.sign(h,k)
req.sendall(b'Message signed:\n' +\
msg.hex().encode() + b'\n' + \
b'Signature:\n' + \
hex(r)[2:].encode() + b',' + hex(s)[2:].encode() +b'\n')
we see it is printed out for the user!
That means that any message we have signed, we are given the value of $k$ that was used. If we look at the math responsible for creating part of the signature $(r,s)$ we see that \[ s = k^{-1}(H(m) + xr) \mod{q} \] Where $x$ is the private key, $H(m)$ is the value of the hashed message, $q$ is a parameter in the public key, and $r$ and $s$ constitute the signature. This is why $k$ needs to be kept a secret, because we now have one equation and only one unkown, the private key. So just like 7th grade algebra, we can solve for $x$ and then we will be able to create a signature valid for this keypair for any message we want. Bearing in mind that since we are working over the integers mod $q$ division is accomplished by the multiplication of inverses (link if you are new to modular arithmetic) \[ \begin{align} s \equiv k^{-1}(H(m) + xr) &\pmod{q} \\ sk \equiv H(m) + xr &\pmod{q} &\text{“divided” by $k$} \\sk - H(m) \equiv xr &\pmod{q} &\text{subtracted $H(m)$} \\r^{-1}(sk - H(m)) \equiv x &\pmod{q} &\text{“divided” by $r$} \end{align} \]
I came, I saw, I conquered
All we need to do now is plug and chug, so let’s grab the public key,
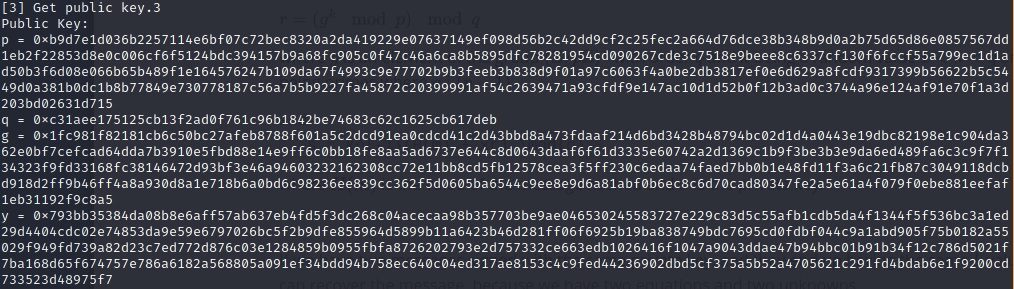
sign a message,

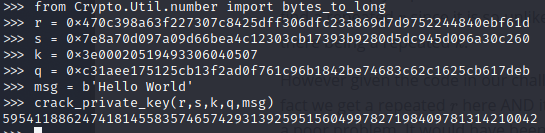
and input the appropriate values into the forumula to solve for the private key. I used the function below.
def crack_private_key(r, S, k, q, msg):
h = bytes_to_long(SHA.new(msg).digest())
k = k % q
r_inv = pow(r, -1, q)
x = r_inv * (S * k - h)
return x % q
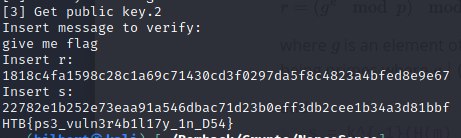
Now that we have the value for the private key we can use pycrptodome to sign the message ‘give me flag’. [doc1][doc2] [src]
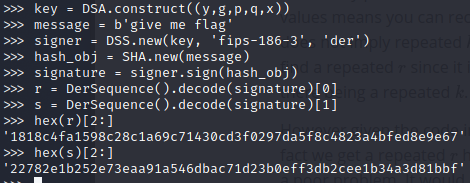
and use the signature to retrieve the flag
BONUS:
Wondering what that secret key the server was using was??
msg = [ a ^ b for (a,b) in zip(msg, cycle(KEY)) ]
Even if they hadn’t so nicely printed out the value of $k$ for us, this is still a terribly insecure implementation and would be trivial to break. The value for $k$ is dependent on the size of the message, send a single byte and $k$ ends up as a value between 0-255. You could brute force that with your trusty TI-85! Even without knowing what algorithm was being implemented you could quickly find out there is a problem with some fuzzing. Look what happens when we send it this single character, even with me doing their job for them and hiding the value of $k$ it’s clear this is b0rked.
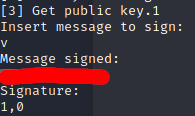
This happens because ‘v’ is the value of the first character of the key. Anything XORed with itself is zero. With $k = 0$ the solution to $r =(g^{k} \mod{p}) \mod{q}$ is simply 1. We can use the fact that anything XORed with zero is itself to retrieve the value of KEY. We simply send a bunch of null bytes (CTRL-SHIFT-@) and voila
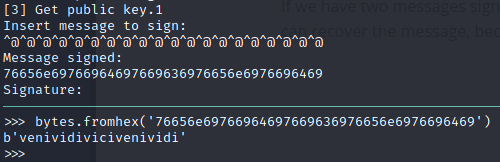
a key 12 whole bites long before repeating. venividivinci indeed!
fun fact: There wasn’t any checking, so you could have entered $(1,0$) as the signature for any message and it would have validated! That would have been a much shorter write-up however, and thanks to the magic of voodoo all the minutes I get people to waste reading this are added on to my life.
Bonus fun fact: This challenge has a great deal in common with the active HTB crypto challenge Signup, so if you didn’t solve this one and want a shot at redemption or are simply hungry for some more DSA head over there and give it a go.
Source
I’m not sure if this challenge will end up in the retired crypto section on HTB, so I am including the server.py code below so you can run it if you so desire. Also I included a copy of the code I wrote for retrieving the flag programatically.
server.py
from Crypto.Util.number import *
import Crypto.PublicKey.DSA
from Crypto.Hash import SHA
import socketserver
import signal
import time
from itertools import cycle
from secret import KEY, FLAG
class DSA:
def __init__(self):
self.pKey = Crypto.PublicKey.DSA.generate(2048)
def get_k(self, msg):
kmax = self.pKey.q
msg = [ a ^ b for (a,b) in zip(msg, cycle(KEY)) ]
msg = bytes(msg)
k = bytes_to_long(msg) % self.pKey.q
return msg, k
def sign(self,h,k):
r = pow(self.pKey.g,k,self.pKey.p)%self.pKey.q
try:
s = (inverse(k, self.pKey.q) * (h+ self.pKey.x * r)) % self.pKey.q
return r, s
except ZeroDivisionError:
return None
def verify(self, m, r, s):
w = inverse(s, self.pKey.q)
m = bytes_to_long(SHA.new(m).digest())
u1 = (m * w) % self.pKey.q
u2 = (r * w) % self.pKey.q
v = (pow(self.pKey.g, u1, self.pKey.p) * pow(self.pKey.y, u2, self.pKey.p)) % self.pKey.p % self.pKey.q
if v == r:
return True
return False
def challenge(req):
dsa = DSA()
while True:
try:
req.sendall(b'Welcome to beta signing system of Best CA LTD.\n'+\
b'[1] Sign a message.\n' +\
b'[2] Verify a message.\n' +\
b'[3] Get public key.')
opt = req.recv(4096).decode().strip()
if opt=='1':
req.sendall(b'Insert message to sign:\n')
msg = req.recv(4096).strip()
if msg ==b'give me flag':
req.sendall(b'Forbidden message!\n')
continue
h = SHA.new(msg).digest()
msg,k = dsa.get_k(msg)
h = bytes_to_long(h)
r, s = dsa.sign(h,k)
req.sendall(b'Message signed:\n' +\
msg.hex().encode() + b'\n' + \
b'Signature:\n' + \
hex(r)[2:].encode() + b',' + hex(s)[2:].encode() +b'\n')
elif opt=='2':
req.sendall(b'Insert message to verify:\n')
msg = req.recv(4096).strip()
req.sendall(b'Insert r:\n')
r = int(req.recv(4096).strip(), 16)
msg ==b'give me flag'
req.sendall(b'Insert s:\n')
s = int(req.recv(4096).decode().strip(), 16)
if dsa.verify(msg,r,s):
if msg == b'give me flag':
req.sendall(FLAG + b'\n')
exit(1)
else:
req.sendall(b'Valid signature.\n')
else:
req.sendall(b'Invalid signature.\n')
elif opt=='3':
req.sendall(b'Public Key:\n' +\
b'p = ' +hex(dsa.pKey.p).encode() + b'\n' + \
b'q = ' +hex(dsa.pKey.q).encode() + b'\n' + \
b'g = ' +hex(dsa.pKey.g).encode() + b'\n' + \
b'y = ' +hex(dsa.pKey.y).encode() + b'\n')
else:
req.sendall( b'Invalid option!')
exit(1)
except Exception as e:
req.sendall(b'Invalid Input. Exit!')
exit(1)
class incoming(socketserver.BaseRequestHandler):
def handle(self):
signal.alarm(300)
req = self.request
while True:
challenge(req)
class ReusableTCPServer(socketserver.ForkingMixIn, socketserver.TCPServer):
pass
socketserver.TCPServer.allow_reuse_address = True
server = ReusableTCPServer(("0.0.0.0", 23333), incoming)
server.serve_forever()
solution.py
import Crypto.PublicKey.DSA
from Crypto.Util.number import *
from pwn import *
from Crypto.Hash import SHA
from itertools import cycle
# This is just a copy of the DSA class the server is using so
# we can easily sign messages. All I did was change the constructor
# to create a specifc key instead of a random one as well as get rid
# of the other functions as they are unneeded.
class DSA:
def __init__(self, key):
self.pKey = Crypto.PublicKey.DSA.construct(key)
def sign(self,h,k):
r = pow(self.pKey.g,k,self.pKey.p)%self.pKey.q
try:
s = (inverse(k, self.pKey.q) * (h+ self.pKey.x * r)) % self.pKey.q
return r, s
except ZeroDivisionError:
return None
# returns all ints
def get_msg_signature(conn, msg):
conn.writeline(b'1')
conn.readline()
conn.writeline(msg)
output = conn.readuntil(b'[3] Get public key.').decode().split('\n')
k = int(output[1], 16)
r = int(output[3].split(',')[0], 16)
s = int(output[3].split(',')[1], 16)
return k, r, s
# input is all bytes
def get_flag(conn, msg, r, s):
conn.writeline(b'2')
conn.readline()
conn.writeline(msg)
conn.readline()
conn.writeline(r)
conn.readline()
conn.writeline(s)
flag = conn.readline()
return flag.decode()
# returns all ints
def get_public_key(conn):
conn.writeline(b'3')
output = conn.readuntil(b'[3] Get public key.').decode().split('\n')
p = int(output[1].split(' = ')[1], 16)
q = int(output[2].split(' = ')[1], 16)
g = int(output[3].split(' = ')[1], 16)
y = int(output[4].split(' = ')[1], 16)
return p,q,g,y
# returns int
def crack_private_key(r, S, k, q, msg):
h = bytes_to_long(SHA.new(msg).digest())
k = k % q
r_inv = pow(r, -1, q)
x = (S * k - h) * r_inv
return x % q
LOCAL_HOST = '127.0.0.1'
LOCAL_PORT = 23333
#HOST = '138.68.155.238'
#PORT = 31867
FLAG_MESSAGE = b'give me flag'
def main():
#conn = remote(HOST, PORT)
conn = remote(LOCAL_HOST, LOCAL_PORT)
conn.readuntil(b'[3] Get public key.')
p, q, g, y = get_public_key(conn)
msg = b'Hello World'
k, r, s = get_msg_signature(conn, msg)
x = crack_private_key(r, s, k, q, msg)
dsa = DSA((y,g,p,q,x))
h_flag = bytes_to_long(SHA.new(FLAG_MESSAGE).digest())
r_flag, s_flag = dsa.sign(h_flag, 42) #you can put anything you want for k
flag = get_flag(conn, FLAG_MESSAGE, hex(r_flag)[2:].encode(), hex(s_flag)[2:].encode())
print(flag)
if __name__ == '__main__':
main()
If you found this walkthrough helpful, please consider adding a respect to my profile, thanks.